Functies
 

Weet iemand hoe ik deze som moet aanpakken?

Stel de formule op van het punt E(15.0) Die evenwijdig is met de lijn door punt F(7,4) en G(20,-22)

Bedoel je misschien de vergelijking van de lijn door E, evenwijdig met de lijn door F en G?

Ja. Ik snap alleen nooit welk punt je van welk punt moet aftrekken om de delta uit te rekenen

Je mag kiezen (verschil van de y-coördinaten delen door het verschil van de x-coördinaten), als je in teller en noemer maar hetzelfde doet. Dit geeft je de richtingscoëfficiënt van de rechte door F en G, je moet dan de vergelijking opstellen van een rechte met gegeven rico en door het punt E.

Bekijk het volgende plaatje eens:http://img9.imageshack.us/my.php?image=lineair.jpg
Op deze manier kun je het richtingcoefficient van de functie bepalen, je hoeft daarna alleen nog de constante B te berekenen.

het richtingscoefficient is natuurlijk delta y delen door delta x, en niet delta x delen door delta y, mijn fout.

Er zijn 2 manieren. De eerste manier is de volgende: bepaal de r.c. van de lijn door F(x_F,y_F) en G(x_G,y_G) met behulp van de formule 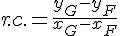. Stel dat dit de waarde a is, dan heeft de lijn door E de vergelijking y=a*x+b. Omdat y_E=0 vind je: a*x_E+b=0, dus b=-a*x_E, dus de lijn door E heeft de vergelijking y=a*x-a*x_E=a(x-x_E). Algemeen geldt: als de lijn met r.c. a door het punt (p,q) gaat heeft deze lijn de vergelijking y-q=a(x-p). Dit wordt de punt-richtingsvergelijking van de lijn genoemd. Je kunt deze punt-richtingsvergelijking afleiden door x=p en y=q in y=a*x+b in te vullen en daaruit b op te lossen.
De tweede manier is de volgende: stel y=a*x+b is de gevraagde vergelijking van de lijn door E en F, dan moet gelden: y_F=a*x_F+b en y_G=a*x_G+b, dus b=y_F-a*x_F en b=y_G-a*a*x_G, dus y_F-a*x_F=y_G-a*x_G, dus a(x_G-x_F)=y_G-y_F, dus 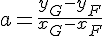. De verdere aanpak is als bij de eerste manier.