[NA] Arbeid in Radiaal veld

[Metric]

Hallo,
We moesten voor natuurkunde deze oefening maken, helaas hebben we nog geen oefening in deze stijl gedaan en weet ik dus iet hoe je moet beginnen. Als iemand me een beetje zou kunnen helpen..

Bewijs dat de arbeid die de veldkracht levert, als een testlading in het radiaal veld van de figuur van a naar b gaat, dezelfde is als men de baan a-c-b of de baan a-d-b volgt.

Figuur:

[ILUsion]

Je veld is radiaal gericht, dat wilt zeggen dat


Arbeid, is per definitie volgende integraal:


De arbeid geleverd door het veld is dus:


Die integraal kan je gaan uitwerken, ik heb daar geen zin in in ieder geval; maar je kan zo al zien dat als je de radiale kracht projecteert (via het dot-product) op een korte lijnvector die loodrecht op die radius staat (zoals het geval in ad en cd), je nul krijgt; dus op die stukken geeft die integraal 0.Dat is het algemeen geval; maar je kan die integraal makkelijker uitwerken als je die gewoon uitwerkt voor beide paden, en dan elk pad in twee splitst (het ene deel geeft 0, het andere deel geeft de arbeid).

[Metric]

Zo 'n dingen hebben wij nog helemaal niet geleerd. Althans, het deel van die integralen. Dus, ik denk dat er een andere manier moet zijn, anders zou onze leerkracht die oefening nog niet hebben opgegeven.

Waarschijnlijk moet je het wel via de integralen doen, maar dan meer "begrijpen" in plaats van uitrekenen. Wat je je hier moet realiseren is dat er, omdat het veld radiaal gericht is, geen arbeid wordt geleverd wanneer je een cirkelbaan aflegt. De arbeid wordt slechts geleverd als je een pad aflegt in radiale richting, en die arbeid is hetzelfde omdat het krachtveld alleen een functie is van de afstand tot het middelpunt (ik neem aan dat de banen a d en c b cirkelbanen zijn).

[ILUsion]

De truc blijft eruit bestaan om elk pad in 2 stukken te delen: een pad dat radiaal loopt en een pad dat volgens de cirkelomtrek loopt en op beide de arbeid uitrekenen. Volgens die cirkelomtrek, levert het radiaalveld geen arbeid, want je beweegt volgens de cirkel en de kracht is radiaal, dus ze staan loodrecht op elkaar (de raaklijn aan een cirkel en de straal van de cirkel staan loodrecht op elkaar); dus als je het ene projecteert op het andere, krijg je 0. Langs de andere kant, komt die projectie wel uit en perfect: je beweegt perfect radiaal en je kracht is perfect radiaal.

Je kan het een beetje als volgt bekijken: je rijdt met een fiets over die lijnen van a naar b en in het middelpunt van je cirkels blaast een ventilator radiaal wind (je radiaal veld); als je je radiaal beweegt, krijg je wind in de rug, dus de kracht van het radiaal veld zal helemaal in arbeid overgaan: je zou kunnen stoppen met trappen en de wind al het werk laten doen. Langs de andere kant, als je over een cirkelbaan gaat, heb je wind langs je zijkant (oke, die blaast je misschien omver, maar dat gebeurt niet want je bent vastberaden dat pad te volgen), dus zal de wind op dat moment geen arbeid leveren: je moet zelf al het werk doen om vooruit te gaan op dat pad.

[Metric]

ILUsion schreef:

Je kan het een beetje als volgt bekijken: je rijdt met een fiets over die lijnen van a naar b en in het middelpunt van je cirkels blaast een ventilator radiaal wind (je radiaal veld); als je je radiaal beweegt, krijg je wind in de rug, dus de kracht van het radiaal veld zal helemaal in arbeid overgaan: je zou kunnen stoppen met trappen en de wind al het werk laten doen. Langs de andere kant, als je over een cirkelbaan gaat, heb je wind langs je zijkant (oke, die blaast je misschien omver, maar dat gebeurt niet want je bent vastberaden dat pad te volgen), dus zal de wind op dat moment geen arbeid leveren: je moet zelf al het werk doen om vooruit te gaan op dat pad.

Maar dan is de arbeid a-b toch niet gelijk aan a-c-b of a-d-b?
Want bij a-c-b of a-d-b is die arbeid dan 0.
Maar bij a-b is die niet gelijk aan 0, want het gaat helemaal in arbeid over.

[ILUsion]

Metric schreef:

Maar dan is de arbeid a-b toch niet gelijk aan a-c-b of a-d-b?
Want bij a-c-b of a-d-b is die arbeid dan 0.
Maar bij a-b is die niet gelijk aan 0, want het gaat helemaal in arbeid over.

Juist wel. Het is niet dat omdat je eventjes over een cirkelbaan gaat dat de totale arbeid nul wordt; het is enkel op de cirkelbaan dat je deeltje arbeid nul wordt. Ik weet niet of je al integralen gezien hebt, maar dat is gewoon het splitsen van een integraal, eigenlijk is daar weinig spectaculairs aan. En als je nog geen integralen gezien hebt, het is vooral een duur woord voor een som: in dit geval bereken je op elk punt van je baan wat de geleverde arbeid is op dat puntje en je telt alles op.

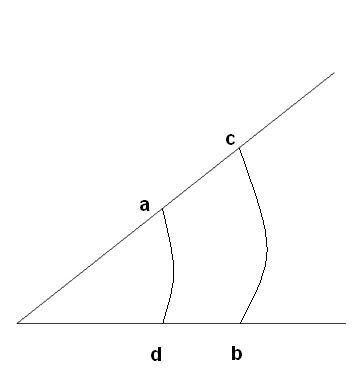
De arbeid over a-c-b = de arbeid over a-d-b = de arbeid over a-b (dat laatste is enkel moeilijker uit te leggen. Bij a-b beweeg je namelijk niet-radiaal: het middelpunt heb je daar getekend, je verandert zowel de afstand tot dat middelpunt (=radiaal) als de hoek (=niet-radiaal) t.o.v. dat middelpunt als je rechtstreeks a-b afloopt. Om het even welke weg je volgt van a naar b, de arbeid zal constant zijn (en gelijk aan de arbeid van a-c = arbeid d-b). Want al de rest van afstand dat je aflegt is loodrecht op de kracht.

Misschien helpt het als je een betere tekening maakt, want degene die je nu hebt is echt wel scheef. Nog op een andere manier uitgelegd: als je recht van het middelpunt weggaat of er recht naar toegaat, levert dat radiaal veld alle arbeid. Als je je daarentegen verplaatst, maar even ver van het middelpunt blijft, heeft je radiaal veld geen arbeid geleverd. Het tussenliggende geval is dan weer complexer (en het veld gaat dan een deel van de arbeid leveren).

En nog een andere manier: je kent waarschijnlijk al wel cartesische assen (x- en y-as), nu de assen die je hier gebruikt zijn polaire assen (een radiale as en een hoek-as). Net zoals in cartesische coördinaten: als je kracht volgens x is en je beweegt volgens y, dan levert de kracht geen arbeid. Hier is dat hetzelfde: als de kracht volgens de radiaal-as loopt, levert die arbeid, en geen arbeid volgens de hoek-as. Probeer alleen niet te hard om de radiaal-as en hoek-as te tekenen, want dat is niet zo simpel. En dat vergelijk tussen x- en y-as en de polaire assen, geldt in dit geval. Je mag dat niet voor alle assen doen (hier mag dat omdat de x-as en de y-as loodrecht op elkaar staan en de polaire assen staan ook loodrecht op elkaar).

Ik hoop dat je het nu doorhebt