[WI] Log & ln

boku · **06-03-2012, 18:42**

Kan iemand mij een paar dingen uitleggen over de logaritmen en de natuurlijke logaritme? de uitleggen van wikipedia zijn nog net iets te hoog gegrepen en ik weet niet welke andere bronnen goed zijn hiervoor. de toepassing van log ken ik nog wel, maar ik weet niet meer precies waarvoor ze precies nuttig zijn

waarvoor worden beide gebruikt?
wat is die wiskundige constante e uit de natuurlijke logaritme? wat voor functie heeft die?

the economist · **07-03-2012, 00:41**

basis is het belangrijkste.
soms wil je in een vergelijking het machtsgetal uitrekenen.
8 = 2^x
hoeveel is x dan.?
dit doe je met het logaritme: 2 log 8 = 3.
"tot welke macht moet je 2 verheffen om 8 te krijgen ? => 3

het is dus de omgekeerde bewerking, net als plus en min, delen en vermenigvuldigen

via de rekenregels van de logaritmen, met grondtallen veranderen en zo, zie elders, kun je het antwoord, hierboven dus 3, vinden.

ThomasJu · **07-03-2012, 07:17**

Als eerste werd e geïntroduceerd bij mij in het hoofdstuk over de afgeleide. de afgeleide van e^x is namelijk hetzelfde!

De ln wordt vaak gebruikt. voor verschillende toepassingen. Zo wordt ln(2) gebruikt bij exponentiële groei. Je zal vanzelf meer dingen tegenkomen waar het voor wordt gebruikt.

Siron · **07-03-2012, 15:47**

In vele gevallen wordt het getal van Euler geintroduceerd als:
$\lim_{x \to +\infty} \left(1+\frac{1}{x}\right)^x=e$

Indien je wat weet over limieten is hoogstwaarschijnlijk je eerste reactie dat deze limiet gelijk is aan $+\infty$ (toepassen van limietwaarde=functiewaarde). Echter wanneer je naar de rij gaat kijken met algemene term $\left(1+\frac{1}{n}\right)^n$ , nl de rij
$2,2.25, 2.37037,2.4414, \ldots$
dan zal deze rij niet divergen, maar convergeren naar (zogenoemde) getal van Euler: $e=2,71828 \ldots$ en blijkbaar heeft dit irrationaal getal meer interessante eigenschappen dan de meeste andere getallen. Eerst en vooral (zoals al aangehaald is in de vorige post) is de afgeleide van $e^x$ gelijk aan zichzelf. Verder vind je het getal van Euler in bekende formules zoals de formule van Euler: $e^{ix}=\cos(x)+i\sin(x)$ en wordt het gebruikt als grondtal voor de logaritme wat de neperse of natuurlijke logaritme genoemd wordt.

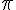
Je kan je eigenlijk hetzelfde afvragen over het getal $\pi$ dat is ook een irrationaal getal met bijzondere eigenschappen.

Mr.Mark · **08-03-2012, 16:35**

Gewoon dit onthouden:

$2^{3}=8<br /> \sqrt[3]{8}=2$
$^{2}log(8)=3$

07-03-2012, 07:17
ThomasJu	Als eerste werd e geïntroduceerd bij mij in het hoofdstuk over de afgeleide. de afgeleide van e^x is namelijk hetzelfde! De ln wordt vaak gebruikt. voor verschillende toepassingen. Zo wordt ln(2) gebruikt bij exponentiële groei. Je zal vanzelf meer dingen tegenkomen waar het voor wordt gebruikt.

08-03-2012, 16:35
Mr.Mark	Gewoon dit onthouden: $2^{3}=8<br /> \sqrt[3]{8}=2$ $^{2}log(8)=3$ __________________ 's Avonds een vent, 's ochtends absent.

Advertentie