Citaat:
|
ok, er is iets wat ik nog niet begrijp:
als je x^5 + x^4 + x^3 + x^2 + x + 1 deelt door (x+1) dan krijg je toch x^4 + x^2 + 1 !?
|
Even controleren of dit klopt: (x+1)(x
4+x²+1)=x
5+x
3+x+x
4+x²+1
=x
5+x
4+x
3+x²+x+1. Dit klopt, dus de deling is correct uitgevoerd.
Citaat:
|
hoe kom je dan bij (x+1) (x²+a*x+1) (x²+b*x+1) ?
|
Het idee is dat je x
4+x²+1 als het product van 2 kwadratische veeltermen schrijft. Je gaf zelf al aan hoe het antwoord er uit moest zien, vandaar dat je x
4+x²+1 als (x²+a*x+1)(x²+b*x+1) probeert te schrijven om zo a en b te vinden. Je kunt de kwadratische veeltermen ook als volgt vinden: er geldt namelijk: x
4+x²+1=x
4+x²+1+x²-x²=x
4+2*x²+1-x²=(x²+1)²-x²=(x²+1-x)(x²+1+x)
=(x²-x+1)(x²+x+1).
Citaat:
|
en er is nog een oefening die ik niet snap: het gaat over willekeurige driehoeken (cosinusregel, sinusregel )
twee krachten F1=24 N en F2=38N grijpen aan in eenzelfde punt en sluiten een hoek van 47graden24'30" in.
bereken de grootte van de resultante en de hoek die de resultante met de grootste kracht insluit.
om te beginnen; wat is een resultante? als ik dat weet kan ik het misschien wel oplossen maar leg het mischien anders toch nog maar eens uit ...
het antwoord moet zijn: 57N en 18graden'07'37"
|
Dit is weliswaar nogal offtopic, maar vooruit: als je een aantal krachten vectorieel optelt stelt de somvector van deze krachten de resultante voor. Je weet dat de 2 krachten in hetzelfde punt aangrijpen en je weet welke grootte ze hebben en welke hoek ze met elkaar maken. De 2 krachten vormen 2 aanliggende zijden van een (krachten)parallellogram, waarbij de resultante de diagonaal van dit parallellogram met hetzelfde aangrijpingspunt als de 2 krachten voorstelt. Laat F
r de grootte van de resultante zijn, dan geldt volgens de cosinusregel: F
r²=24²+38²+2*24*38*cos(47°24'30"). Laat
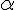
de gevraagde hoek tussen de grootste kracht en de resultante zijn, dan geldt:
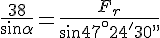
.

 Soortgelijke topics
Soortgelijke topics



 Danku.
Danku.

 Adverteren
Adverteren