[WI] Delen

kleine getal gedeeld door grote getal.

bijvoorbeeld:

70/262
24/52
32/64
etc.

70/262=(2x35)/(2x131)
24/52=(2x12)/(2x26)=(2x2x2x3)/(2x2x13)=6/13
32/64=(32)/(2x32)=1/2

nu jij:
70/812=..

Hoe verander je een breuk naar een x.xxxx getal?

Maar wat ik bedoel, is er een snellere manier? Net als een staartdeling, maar dan omgekeerd?

[mathfreak]

wiskunde_n00b schreef:

Hoe verander je een breuk naar een x.xxxx getal?

Maar wat ik bedoel, is er een snellere manier? Net als een staartdeling, maar dan omgekeerd?

Wat je dus wilt weten is hoe je een gewone breuk in een decimale breuk omzet. Hierbij kunnen zich 2 situaties voordoen: de breuk heeft een eindig aandal decimalen, of de breuk heeft een oneindig aantal decimalen die na verloop van tijd steeds herhaald worden. In dat laatste geval spreken we van een oneindig repeterende decimale breuk.
Een gewone breuk is te schrijven als een eindige decimale breuk als de noemer alleen machten van 2 en 5 als factoren bevat. Als de noemer daarnaast nog andere factoren bevat, dan krijgen we een oneindig repeterende decimale breuk.
Neem bijvoorbeeld de breuk . Deze breuk is te schrijven als .
De breuk is te schrijven als .
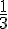
In deze 2 voorbeelden bevatte de noemer alleen factoren van 5, dus kun je, door teller en noemer met een geschikte macht van 2 te vermenigvuldigen, een gewone breuk krijgen met een macht van 10 als noemer, die dus als een eindige decimale breuk te schrijven is. Neem nu echter eens de breuk . Deze breuk is te schrijven als . We moeten dus weten hoe als decimale breuk te schrijven is. Voeren we een staartdeling uit om deze breuk te berekenen, dan krijgen we:

3/1,000...\0,333...
      9
   ----
      10
        9
      ---
         10
           9
         ---
            10
            .
            .
            .

.
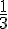
De breuk wordt dus decimaal geschreven als . We vinden dus: . We noemen de breuk een oneindig repeterende decimale breuk met periode 3 en periodelengte 1.
Het is mogelijk om een eindige decimale breuk als een oneindig repeterende decimale breuk te schrijven. Zo is 1 bijvoorbeeld te schrijven als . Dat dit zo is kunnen we als volgt laten zien:
x=0,999...
10*x=9,999...
10*x-x=9*x=9,999...-0,999...=9, dus x=1.
Stel dat we de decimale breuk hebben. Dit is een oneindig repeterende decimale breuk met 25 als voorperiode en 6 als periode. De voorperiode heeft lengte 2 en de periode heeft lengte 1. Als een oneindig repeterende decimale breuk geen voorperiode heeft spreken we van een zuivere periodieke decimale ontwikkeling, en anders van een gemengd periodieke decimale ontwikkeling.
We gaan nu eens kijken hoe we bij een gegeven breuk vast kunnen stellen hoe we de voorperiode en de periode kunnen vinden. Stel a<b en ggd(a,b)=1, waarbij ggd(a,b) de grootste gemeenschappelijke deler van a en b voorstelt. Stel b bevat de factoren 2^u en 5^v, dan is max(u,v), ofwel het maximum van u en v de lengte van de voorperiode. Voor u=6 en b=1 geldt bijvoorbeeld: max(u,v)=max(6,1)=6, omdat 6 het maximum is van 6 en 1. Voor b=2^u*5^v*c, met c niet 1 en ggd(c,10)=1 geldt: de periodelengte n is het kleinste natuurlijke getal n waarvoor geldt: c is een deler van 10ⁿ-1. Voor c=1 heeft de periode de lengte 0, dus dan is als een eindige decimale breuk te schrijven.
Bekijken we opnieuw de de decimale breuk . Deze breuk heeft een voorperiode 25 met lengte 2 en een periode 6 met lengte 1, dus met max(u,v)=2 en c een deler van 10¹-1, dus max(u,v)=2 en c is een deler van 9. Er geldt: . We gaan nu 0,666... als een gewone breuk schrijven door dezelfde methode toe te passen die we gebruikten om aan te tonen dat 0,999...=1. Stel 0,666...=x, dan geldt: 10*x=6,666..., dus 10*x-x=6,666...-0,666...=6, dus 9*x=6, dus , dus , dus a=77 en b=2²*5²*3, dus a=77 en u=v=2 en c=3.